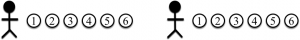Livre Graphes et Algorithmes – Jeux grandeur nature.
Règles du jeu et exemple.
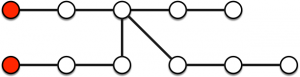
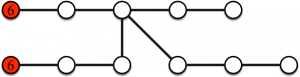
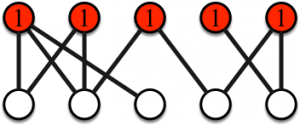
Graphe. Le jeu se déroule avec un graphe quelconque et un ensemble de points de départ représentés par des sommets rouges. Considérons le graphe suivant.
Nombre de joueurs. Le nombre de joueurs est égal au nombre de points de départ (plusieurs points de départ peuvent se trouver sur un même sommet). Dans notre exemple, il y a deux joueurs.
Accessoires. Chacun des joueurs a un certain nombre d’objets en sa possession. Dans l’exemple, les deux joueurs ont chacun six objets en leur possession.
Déroulement du jeu. Au départ les joueurs occupent les sommets de départ (les deux sommets rouges dans l’exemple). Ils déposent un objet sur leur sommet de départ respectif.
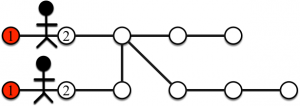
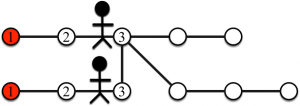
Les joueurs se déplacent, chacun leur tour, sur un sommet voisin et dépose obligatoirement un objet sur le sommet (même si ce sommet contient déjà un ou plusieurs objets). Les joueurs peuvent se retrouver sur un même sommet du graphe au cours du jeu. Le jeu s’arrête lorsque les joueurs n’ont plus d’objet. Pour notre exemple, la figure suivante représente la deuxième étape du jeu. Les entiers sur les sommets représentent les étapes pour lesquelles des objets ont éte déposés.
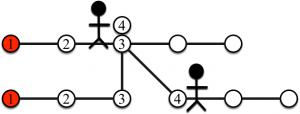
La figure suivante représente la troisième étape du jeu.
La figure suivante représente la quatrième étape du jeu.
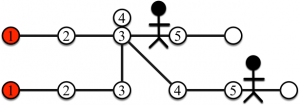
La figure suivante représente l’avant-dernière étape du jeu.
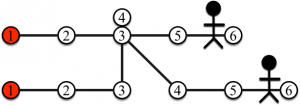
Enfin, la figure suivante représente la dernière étape du jeu. Les deux joueurs ont gagné car tous les sommets ont été visités par au moins un des deux joueurs (c’est-à-dire tous les sommets ont un objet posé dessus).
But du jeu. Lorsque le jeu est terminé (c’est-à-dire lorsque tous les objets ont été déposés sur les sommets), les joueurs ont gagné si et seulement si tous les sommets ont été visités par au moins un joueur (c’est-à-dire s’ils contiennent au moins un objet). Sinon, tous les joueurs ont perdu. Pour notre exemple, les deux joueurs ont gagné car à la fin du jeu (lorsque tous les objets ont été posés) tous les sommets contiennent au moins un objet.
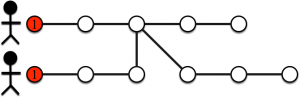
Comment lire les figures qui vont suivre ? Dans la suite, les entiers sur les sommets de départ représenteront le nombre d’objets que possède initialement le joueur partant de ce sommet.
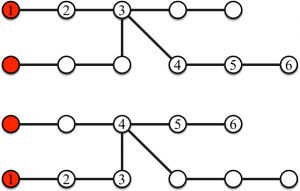
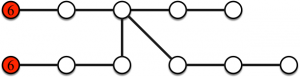
Ensuite, les entiers sur les sommets représenteront les étapes pour lesquelles des objets ont été déposés par les joueurs. Les deux parcours des deux joueurs dans notre exemple sont représentés dans les deux figures suivantes.
Application au calcul de parcours de livreurs
Dans la suite, nous décrivons une des applications possibles du problème de parcours dans les graphes (vous pouvez facilement en trouver d’autres). Les sommets rouges de départ peuvent représenter les positions de livreurs. Ces derniers doivent livrer une information (ou un bien) à toutes les destinations. Les destinations sont les sommets du graphe et les arêtes sont les possibles routes pour aller d’un sommet à un autre. Les livreurs peuvent parcourir un nombre limité de sommets (ce sont les nombres sur les sommets). Lorsqu’un livreur est sur un sommet, alors il livre l’information (ou le bien). Le problème est alors de trouver un parcours pour chacun des livreurs avec l’objectif d’effectuer une livraison à tout le monde. Cela correspond exactement au problème étudié précédemment de parcours dans les graphes.
Graphes pour jouer
Jeu 1. Considérons le graphe suivant avec deux sommets de départ (sommets rouges) et six objets en possession de chacun des deux joueurs. Quelle est la solution pour ce jeu du parcours ?
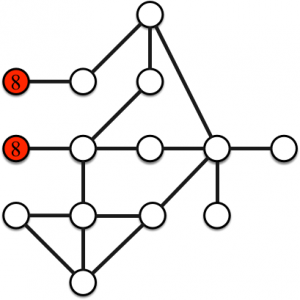
Jeu 2. Considérons le graphe suivant avec deux sommets de départ (sommets rouges) et huit objets en possession de chacun des deux joueurs. Est-ce qu’il existe une solution pour cette instance ? Si non, combien de sommets au minimum n’ont pas d’objet posé dessus à la fin de la partie ?
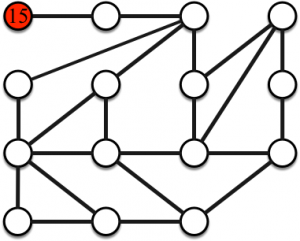
Jeu 3. Considérons le graphe suivant avec un joueur et quinze objets. Ce nombre d’objets est-il suffisant pour parcourir tout le graphe ?
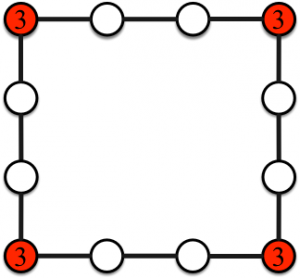
Jeu 4. Les sommets rouges représentent les points de départ et les nombres d’objets pour chacun des joueurs (il y a un joueur par point de départ).
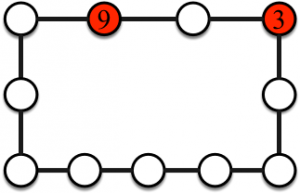
Jeu 5. Les sommets rouges représentent les points de départ et les nombres d’objets pour chacun des joueurs (il y a un joueur par point de départ).
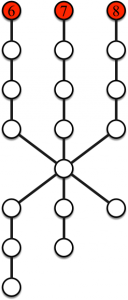
Jeu 6. Les sommets rouges représentent les points de départ et les nombres d’objets pour chacun des joueurs (il y a un joueur par point de départ).
Jeu 7. Les sommets rouges représentent les points de départ et les nombres d’objets pour chacun des joueurs (il y a un joueur par point de départ).
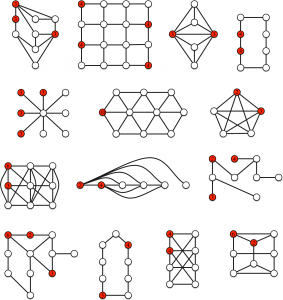
Jeux 8 à 21. Les figures suivantes décrivent quatorze jeux du parcours.